Drodzy Czytelnicy!

‍

7 lutego obchodziliśmy dzień liczby e. Siódmy dzień lutego w amerykańskim zapisie to 2/7 stąd data tego matematycznego i nietypowego święta. Zostało ono wymyślone w 2018 roku przez Amerykanina
Rona Gordona, który długie lata uczył matematyki w szkole średniej w Redwood City w Kaliforni.
Pan Gordon słynie również jako ogromny entuzjasta matematyczny i pomysłodawca wielu innych "liczbowych" świąt [1,2,3]

Liczba e, nazywana również liczbą Eulera (czyt. `ojlera) lub Nepera/Napiera (czyt. nej`pijaa),
jest liczbą niewymierną - ma nieskończone rozwinięcie i nie da się jej wyrazić jako ułamek zwykły.

‍

Możemy jedynie mówić o PRZYBLIŻENIACH jej wartości:

- podstawowe, mało dokładne to 2,7

- najczęściej używane to 2,718

- dokładniejsze to 2,71828

- używając przekornie ułamka zwykłego to 19/7, 87/32 albo 193/71

- zaś tablicowe to 2,718 281 828 459 045 235 360 287 471 352 266 249 775 724... [4]

- rekordowe przybliżenie liczby e wyliczone w 2020 roku zawiera ponad (polskie) 31 bilionów znaków [5]

‍

Ciekawostką jest to, że w 2023 roku, Hindus Deepu V pobił Światowy Rekord Guinessa i z pamięci wyrecytował 14 000 cyfr liczby e! Zajęło mu to 49 minut [6].

‍

‍

Liczba e jest więc niewymierna, podobnie jak liczba pi. Liczba e ma również ogromne znaczenie filozoficzne i matematyczne, podobnie jak liczba pi. Obie te liczby mają też dużo wspólnego ze sobą.

Z jednej strony e opisuje statystyczność, a z drugiej strony pi opisuje okresowość. Nic więc dziwnego,
że te dwie liczby rządzą naszym światem i wszelkimi procesami matematycznymi, ekonomicznymi, chemicznymi, fizycznymi, biologicznymi...

‍

Skąd wzięła się ta liczba?

Szkocki szlachcic i matematyk John Napier (łac. Ioannes Neper) w XVII wieku badał i ustanowił pojęcie logarytmu. Już wtedy było jasne, że procesami w Przyrodzie rządzą linie związane z jedną i tą samą tajemniczą liczbą - Liczbą Natury, Logarytmem Naturalnym [7].

‍

Później, również w XVII wieku, helwecki patrycjusz i matematyk, Jacob Bernoulli (tak, ten od ciągów, nierówności czy mechaniki płynów) dołożył swoją cegiełkę do tej tajemniczej liczby,
wyznaczając ją jako 2.5<e<3.0 [9].

O rodzinie Bernoullich, dynastii geniuszów, z pewnością jeszcze usłyszymy ;)

‍

Liczba e została nazwana na cześć Leonharda Eulera (1707-1783), oświeceniowego szwajcarskiego polimata, który był jej słynnym badaczem. Dokonał przełomowego oznaczenia 23 cyfr liczby e.
Zdefiniował również matematycznie liczbę e jako granicę ciągu oraz wprowadził ją do podstawy logarytmu naturalnego [10].

Rozpropagował też zapis liczby pi za pomocą greckiego "p" [10].
Niewymierny przypadek? Nie sądzimy ;)

‍

‍

‍

Euler był niesamowitą wybitnością w swoich czasach, największym matematykiem i utrzymał to miano do dzisiaj, do czasów cyfryzacji. Jego nazwisko stoi w jednym szeregu z Leibnizem, Laplace`m, Gaussem, Newtonem, Kartezjuszem, Euklidesem, Archimedesem...

Szwajcar wniósł rewolucyjne prace do niemal każdego działu matematyki: od notacji i algebry poczynając, poprzez geometrię, trygonometrię, różniczki i całki, na teorii liczb kończąc.
Analiza matematyczna wiele mu zawdzięcza, podobnie jak astronomia i logika.

Szczególnie warto wspomnieć o Wzorze Eulera, który wiąże liczby zespolone oraz geometrię z liczbą e:

‍

‍

‍

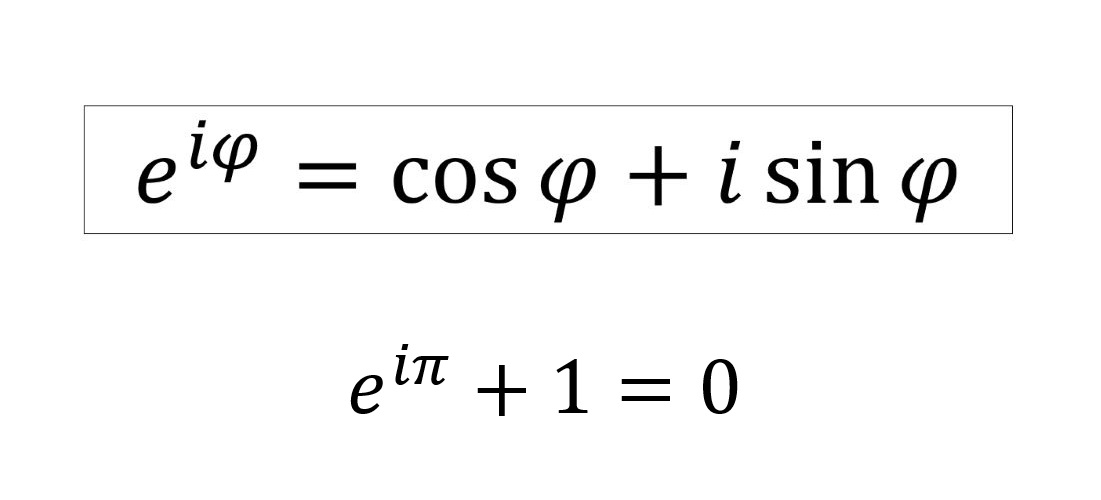
Wzór ten robi wrażenie na każdym nieco wtajemniczonym.

Richard Feynman* nazwał go "najwspanialszym wzorem matematyki" i "naszym klejnotem" [12].

‍

‍

Czy wiecie, że Pan Konrad jest wielkim entuzjastą liczby e? :)))

Zapraszamy na zajęcia!

‍

‍

‍

‍

źródła:

[1] https://mathsquery.com/knowledge/history/important-days-in-math/

[2] https://www.daysoftheyear.com/days/e-day/

[3] https://timesofindia.indiatimes.com/city/mumbai/american-math-teacher-invites-indians-to-blow-the-trumpet-on-2/2/22/

[4] Małe Tablice Matematyka, W. Mizerski, wyd. Adamantan, Warszawa 2019

[5] http://www.numberworld.org/digits/E/

[6] https://www.guinnessworldrecords.com

[7] Ernest William Hobson (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press

[8] https://www.meisterdrucke.pl (faksymile)

[9] Jacob Bernoulli (1690), Quæstiones nonnullæ de usuris, cum solutione problematis de sorte alearum, propositi in Ephem. Gall. A. 1685

[10] Leonhard Euler, Introductio in Analysin Infinitorum (Lausanne, Switzerland: Marc Michel Bousquet & Co., 1748)

[11] Wikimedia Commons (Gunther/Wereon 2006-2024; Cronholm144 2007; Qniemiec 2010)

[12] Feynmana wykłady z fizyki, tom 1-1, wzór 22.9, R.P.Feynmann, R.B. Leighton, M. Sands, wyd. PWN, Warszawa 2014druk/2022ebook

[13] https://www.snb.ch/en/the-snb/mandates-goals/cash/all-series
‍

* - R. Feynman to wybitny fizyk naszych czasów, znakomity dydaktyk,
autor kompendium obecnej wiedzy fizycznej.
Pan Konrad uczy z jego podręczników.

‍

‍

[14.02.2025]

‍